Fungsi Logaritma

Setiap fungsi eksponensial f(x) = ax, dengan a > 0 dan a ≠ 1, merupakan fungsi korespondensi satu-satu. Hal ini dapat dilihat dengan menggunakan Uji Garis Horizontal (lihat Gambar 1 untuk kasus a > 1). Oleh karena itu fungsi eksponensial memiliki fungsi invers. Fungsi invers tersebut dinamakan fungsi logaritma dengan basis a dan dinotasikan dengan loga.

REPORT THIS AD

Fungsi invers f–1 didefinisikan sebagai

Definisi ini akan membawa kita kepada definisi fungsi logaritma berikut ini.

---

Definisi Fungsi Logaritma

Misalkan a adalah bilangan positif dengan a ≠ 1. Fungsi logaritma dengan basis a, yang dinotasikan dengan loga, didefinisikan dengan

Sehingga loga x merupakan pangkat dari a untuk menjadi x.

---

Ketika kita menggunakan definisi logaritma untuk mengganti bentuk logaritma loga x = ymenjadi bentuk eksponensial ay = x, atau sebaliknya, perhatikan bahwa dalam kedua bentuk ini, basisnya tetap sama.

Contoh 1: Bentuk Logaritma dan Eksponensial

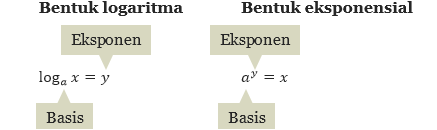
Bentuk logaritma dan eksponensial merupakan persamaan-persamaan yang ekuivalen: Jika bentuk yang satu benar, maka bentuk yang lainnya juga benar. Sehingga kita dapat mengubah bentuk logaritma menjadi bentuk eksponensial, atau sebaliknya, seperti ilustrasi berikut.