VEKTOR DI R2

Vektor di R^2

Panjang segmen garis yang menyatakan vektor  atau dinotasikan sebagai Panjang vektor sebagai:

Panjang vektor tersebut dapat dikaitkan dengan sudut  yang dibentuk oleh vektor dan sumbu x. positif.

Vektor dapat disajikan sebagai kombinasi linier dari vektor basis  dan berikut:

Operasi Vektor di R^2

Penjumlahan dan pengurangan vektor di R^2

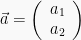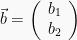Dua vektor atau lebih dapat dijumlahkan dan hasilnya disebut resultan. Penjumlahan vektor secara aljabar dapat dilakukan dengan cara menjumlahkan komponen yang seletak. Jika  dan  maka:

Penjumlahan secara grafis dapat dilihat pada gambar dibawah:

Dalam pengurangan vektor, berlaku sama dengan penjumlahan yaitu:

Sifat-sifat dalam penjumlahan vektor sebagai berikut:

• 
• 

Perkalian vektor di R^2 dengan skalar

Suatu vektor dapat dikalikan dengan suatu skalar (bilangan real) dan akan menghasilkan suatu vektor baru. Jika  adalah vektor dan k adalah skalar. Maka perkalian vektor:

Dengan ketentuan:

• Jika k > 0, maka vektor  searah dengan vektor 
• Jika k < 0, maka vektor  berlawanan arah dengan vektor 
• Jika k = 0, maka vektor  adalah vektor identitas 

Secara grafis perkalian ini dapat merubah panjang vektor dan dapat dilihat pada tabel dibawah:

Secara aljabar perkalian vektor  dengan skalar k dapat dirumuskan:

Perkalian Skalar Dua Vektor di R^2

Perkalian skalar dua vektor disebut juga sebagai hasil kali titik dua vektor dan ditulis sebagai:

 (dibaca : a dot b)

Perkalaian skalar vektor 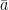 dan 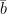 dilakukan dengan mengalikan panjang vektor  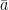dan panjang vektor  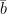dengan cosinus . Sudut  yang merupakan sudut antara vektor 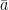dan vektor .

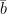Sehingga:

Dimana:

Perhatikan bahwa:

• Hasil kali titik dua vektor menghasilkan suatu skalar
• 
•