 Hasil kali skalar dua vektor
Hasil kali skalar dua vektor
Selain rumus di 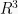 , ada rumus lain dalam hasil kali skalar dua vektor. Jika
, ada rumus lain dalam hasil kali skalar dua vektor. Jika 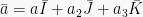 dan
dan  maka
maka 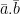 adalah:
adalah:
Proyeksi Orthogonal vektor
Jika vektor 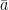 diproyeksikan ke vektor
diproyeksikan ke vektor 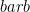 dan diberi nama
dan diberi nama  seperti gambar dibawah:
seperti gambar dibawah:

Diketahui:
Sehingga:
Untuk mendapat vektornya:



0 komentar:
Posting Komentar